Calibration of the Mean BTO Constant
Geoff Hyman and Barry Martin
2015 March 19
(Report prepared in 2014 November)
A downloadable PDF of this report (542 kB) is available here.
Introduction and Summary
We seek to estimate the mean value of K in the BTO equation:
Here TDC refers to the time delay in the C-band (satellite to Perth) signal and TDL to the time delay in the L-band (aeroplane to satellite) signal.
Further details on the calculation of the individual observations may be obtained from Reference [1]. BTO data were available for two types of channel: R and T (Reference [2]). Their associated K values have different means and the offset δ is applied to all of the T-channel observations to allow them to be combined with R-channel observations which maximises the total sample which can be used for estimation. We adopt the convention of setting the offset δ to zero for R-channel observations. The values of K typically vary between observations, so that:
where K-bar is an unknown but constant mean value that we seek to estimate and ε is a residual. For the purposes of calibration the residuals are assumed to be randomly distributed with a mean of zero, have a constant variance, and to be uncorrelated. The value of K-bar is estimated by averaging the K values derived from a suitable sample. In a minor abuse of notation we will also use the symbol K-bar when reporting estimates of its true value, which is unknown.
The plan of this report is as follows. In section 1 preliminary estimates for the mean BTO constant are obtained, examining sensitivity to the magnitude of the T-channel offset and exploring the difference between estimates based on conditions when the aeroplane is stationary with a wider data set when the aeroplane was on the ground. Similar values for the BTO constant were obtained provided the appropriate offsets were re-estimated for the dataset being adopted.
In section 2 a comparison is conducted with estimates published by the ATSB in its June 2014 report. The estimates made there for the mean BTO constant appear to be consistent with our initial findings.
In section 3 some preliminary conclusions are drawn.
In section 4, a review of data from the T-channel is conducted. This resulted in the need to filter out T-channel observations occurring less than a certain critical time after the preceding ones. Consistent estimates for the BTO constant were obtained but with wider confidence limits. We also briefly review a limited data set that includes the climb and early cruise phase, leading to a refinement in the data reduction method.
In section 5 the impact of using a new set of satellite vectors is discussed.
In section 6 a comparison is made between estimates from the reduced data set and estimates based entirely on BTO data for the R-Channel.
In section 7 we revisit the comparison between ATSB’s June estimate for the BTO constant and our latest estimates, using improved satellite position data. The ATSB estimate is also consistent with our revised estimates. It is concluded that the odds were somewhat against ATSB obtaining a value that was as close as was found to our latest estimate, but that this is not a surprising result.
1 Preliminary Estimation
An ensemble of ADS-B logs from numerous feeders [3] provides independent evidence of the aeroplane position history prior to deviation from the flight planned route. The ADS-B position timestamps have an error of ±10 seconds which translates to an along-track error of ±2.4 km, equivalent to an uncertainty in the aircraft-satellite range of the same order, in turn leading to significant BTO prediction errors. For this reason the aerial data were not used in determining the BTO constant.
This issue does not apply when the aeroplane is on the ground because the aeroplane position is well-determined so calibration to ‘ground truth’ will be adopted. Estimation was conducted for periods when MH370 was (a) static; and also (b) still on the ground, but including observations made when the aeroplane was both static and moving.
i) The T-channel offset δ was initially assumed to be 5000 microseconds.
ii) The offset δ value was also optimised to minimise the resulting standard error of the estimated value of K-bar over the combined data for both channels. The resulting offset value was 4979.8 microseconds from 76 data points when the aeroplane was static, and 4976.6 microseconds from 137 data points for the entire period when the aeroplane was on the ground. No outliers were identified at this stage (i.e. all observations in their respective clusters were used).
The estimates for the BTO constant K are given in Table 1 (units in microseconds) using the ATSBX satellite position model. This ATSBX model adopts a linear interpolation for each of the three Cartesian position components for seven vectors given at five-minute intervals over the period 1600 to 1630 UTC in Reference [4] (Appendix G, Table 1).
Further details of the ATSBX model are given in Reference [5] (Vectors).
| ATSBX | Offset δ : 4979.8 μsec | Offset δ : 5000.0 μsec | ||
| Static | Ground (all) | Static | Ground (all) | |
| K-bar | -495679.3 | -495677.5 | -495672.1 | -495665.3 |
| Standard deviation of K | 31.7 | 26.8 | 33.1 | 29.1 |
| Count | 76 | 137 | 76 | 137 |
| Standard error of K-bar | 3.63 | 2.29 | 3.80 | 2.49 |
Table 1: Initial Estimates for BTO constant K (all in microseconds).
Source: [5] (Statistics). All figures in microseconds.
In Table 1 above, and the later tables, the row labelled ‘Standard error of K-bar’ refers to the standard error of the estimate for the mean value of the distribution of the random variable K (cf. the preceding equation for K-bar: K-bar = K + ε). It is closely related to the standard deviation of K, and is calculated using:
Standard error of K-bar = Standard deviation of K / SQRT(Count)
The full ground data set gives a lower standard deviation than the static set. This appears to be because of a greater preponderance of T-channel observations. The variability of K values from the T-channel appears to be much lower than from the R-channel so particular care needs to be taken when combining them in estimates of K-bar. The implications of this issue for estimating K-bar will be investigated in a later section.
When the T-channel offset is set to 5000 microseconds the mean K from the static and full ground data sets differ by 6.8 microseconds. If a standard error 2.49 microseconds (given in the last column of Table 1) was accepted then this difference would be statistically significant. On the other hand, with the optimised T-channel offset, the mean K for the ground set differs by only 1.8 microseconds from the static mean K, which is not statistically significant. To investigate this further the statistics for a T-channel offset of 4976.6 microseconds, estimated from the full ground data, were tabulated in the last two columns of Table 2.
| ATSBX | Static offset δ: 4979.8 μs | Ground offset δ: 4976.6 μs | ||
| Static | Ground (all) | Static | Ground (all) | |
| K-bar | -495679.3 | -495677.5 | -495680.5 | -495679.5 |
| Standard deviation of K | 31.7 | 26.8 | 31.7 | 26.7 |
| Count | 76 | 137 | 76 | 137 |
| Standard error of K-bar | 3.63 | 2.29 | 3.64 | 2.28 |
Table 2: Implications of Static and Ground based offsets for the BTO constant. Source: [5] (Statistics). All figures in microseconds.
Comparing the first and last columns we observe that the mean values for K (both underlined) differ by only 0.2 microseconds. It appears that similar mean K value are obtained irrespective of whether the static or full ground data are used, provided the appropriate T-channel offset is defined for the dataset being adopted, as indicated by the values that are underlined. On this basis the best candidate for the mean BTO constant, in integer microseconds, would be -495679 based on the static data, or -495680 based on the full ground data, with the appropriate T-channel offset in each case. For the purposes of risk analysis, it would be prudent to use the larger standard error of 3.63 obtained for the period when the aeroplane was static.
2 Comparison with ATSB June Estimates
In Reference [4] (Appendix G, Table 2) the ATSB give a mean BTO constant K of -495679(.3) microseconds. The decimal place given in brackets has been calculated from the values given in ATSB’s table and has been included to facilitate comparisons.
This is a fraction of a microsecond away from the value obtained by our analysis, and the difference is not statistically significant. Further examination of the ATSB data indicates that:
a) The ATSB estimate was based on only 17 data points, all from the R-channel;
b) The standard error of the ATSB estimate is 7.6 microseconds, substantially greater than the difference between ATSB’s estimate and those reported here; and
c) The median (50th percentile) of the ATSB values for K is -495661 microseconds, whereas the median for our estimates, from the full ground data, is -495680 so that these median evaluations differ by 19 microseconds.
It is concluded that the close similarity between ATSB’s estimate and ours is fortuitous. In a later section we will make a quantitative assessment of just how likely this might have been.
3 Preliminary Conclusions
Based on the current dataset, using the ATSBX satellite position model, the mean BTO constant is -495680 microseconds, with a standard error of 3.6 microseconds. The 95% normal confidence limits are from -495672 to -495687 microseconds. These estimates will be reviewed in the light of more recent evidence, as presented below.
4 Review of data for the T-Channel
Following comments received from Mike Exner, the T-channel data were examined in more detail. The field ‘SU type’ was found to be associated with several blocks of data referred to as ‘Subsequent Signalling Unit’ (SSU). These were all on the T-channel and came in closely spaced bursts of time. The corresponding K values were closely correlated to the immediately preceding T-channel values, which violates the requirement for the residuals to be uncorrelated within a sample to be used for estimating the value of K-bar . When these were omitted the ground data set was reduced to 61 observations, of which seven were on the T-channel. Optimising the T-channel offset for the reduced data set gave a value of 4983.3 microseconds, as shown in the last column of Table 3a.
| ATSBX | Static | Ground (all) | Reduced |
| Offset δ | 4979.8 | 4976.6 | 4983.3 |
| K-bar | -495679.3 | -495679.5 | -495679.5 |
| Standard deviation of K | 31.7 | 26.7 | 29.8 |
| Count | 76 | 137 | 61 |
| Standard error of K-bar | 3.63 | 2.28 | 3.81 |
Table 3a: Comparison of Static, Ground, and Reduced estimates. Source: [5] (Statistics). All figures in microseconds.
The Reduced data set includes the observations made when the aeroplane was moving on the ground. The BTO constant K-bar from the Reduced data set was -495679.5 microseconds, with a standard error of 3.8 microseconds.
To test the robustness of the filtering process we investigated a wider set of data, extended to 17:08 UTC, which included the climb and early cruise phase of the flight of MH370. This period spanned 497 records, split into 419 on the T-channel and 78 on the R-channel. The data on the T-channel formed 20 clusters. It was found that the SSU reduction method would exclude two exceptional cases, where the recorded BTO value also changed by -40 microseconds A review of the method was therefore warranted. A brief summary of the findings of this review follow.
Even after incorporating the offset the strong serial correlation between successive K values derived from the T-channels presents a dilemma when calculating the descriptive statistics to be used for the estimation. Treating all of the data points as equivalent would:
- Distort the sample mean by giving them excessive weight,
- Violate the requirement that the residuals have constant variance,
- Under-estimate the standard error by exaggerating the effective sample size.
All of these are undesirable features in our current task. For the purpose of estimating the mean BTO constant a practical procedure would be to filter all of the BTO data according to the time interval between observations and take out those with the highest frequency.
This filter only uses the time (UTC) for the observation, obviating the need to have access to the SU type and makes better use of the full set of available data. Analysis of the BTO data extending the ground period into the climb and early cruise phase, up to 17:08 UTC, indicates that a cut-off time interval of the order of 0.35 seconds, applied to the entire data set, would appear to be an effective method for removal of the bulk of T-channel data points which are associated with no changes in sequential K values, whilst retaining all of the K value changes that were observed.
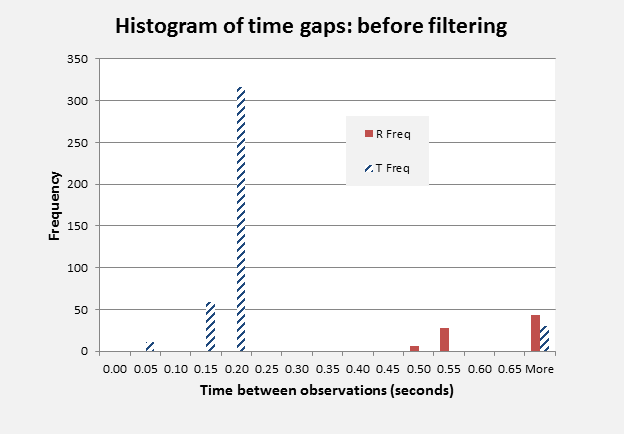
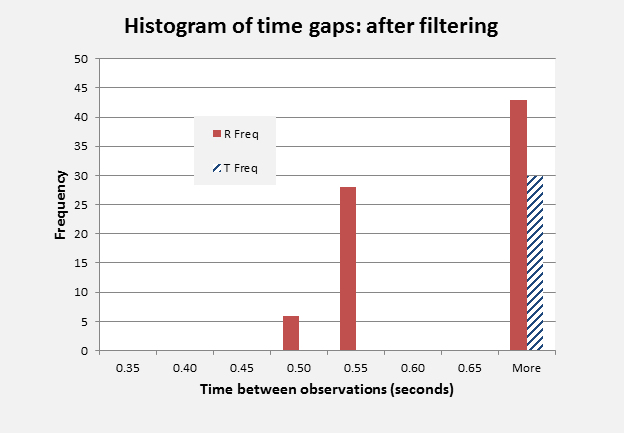
Figure 1: Frequency of time gaps between observations:
before and after filtering. Source: [5](BTO_Tchan)
Figure 1 gives the frequency of occurrence of time intervals between observations within R- and T-channels, shown separately. It can be noted that the R-channel intervals all exceeded 0.45 seconds and there were no inter-observational time intervals between 0.25 and 0.45 seconds on either channel. Application of the cut-off to exclude BTO data that was within 0.35 seconds of a previous data point (irrespective of channel) only removed K values that were part of a closely correlated sequence of values. These were all on the T-channel and a total of 31 T-channel observations were retained in the time filtered data set, corresponding to the count of 30 time increments shown to the right in Figure 1. The retained T-channel data represented the 20 cluster start points and 11 within-cluster points, and included both of the exceptions noted earlier. No R-channel data points were removed in the process.
Returning to our analysis of the ground data, the time-based filter restored one observation to the calibration data set. Table 3b compares the effects on our estimates of the time interval based T- channel filter with the previous filter based on the SU type.
| ATSBX | SU filter | Time filter |
| Offset δ | 4983.3 | 4980.6 |
| K-bar | -495679.5 | -495679.5 |
| Standard deviation of K | 29.8 | 29.6 |
| Count | 61 | 62 |
| Standard error of K-bar | 3.81 | 3.76 |
Table 3b: Comparison of estimates using alternative filters. Source: [5] (Statistics). All figures in microseconds.
One additional T-channel data point was brought into the estimation. This had a noticeable effect on the value for the T- channel offset but had no impact on the value for the estimated mean BTO constant. The standard error of the estimate was marginally reduced.
5 Comparison of impacts of PAR5 and ATSBX Satellite Vectors on the mean BTO constant
New satellite vectors became available allowing recalibration to be conducted with the time-filtered reduced data set. This improved set (PAR5) was obtained from Henrik Rydberg [6] (see also this post). The key statistics are given in Table 4.
| ATSBX | PAR5 | |
| Offset δ | 4980.6 | 4980.3 |
| K-bar | -495679.5 | -495679.0 |
| Standard deviation of K | 29.6 | 29.6 |
| Count | 62 | 62 |
| Standard error of K-bar | 3.76 | 3.75 |
Table 4: Comparison of ATSBX and PAR5 using the time interval filtered data set. Source: [5] (Statistics). All figures in microseconds.
Using PAR5, the optimum T-channel offset for the reduced set of 62 data points was 4980.3 microseconds, a reduction of 0.3 microseconds from the ATSBX value. The new BTO constant was -495679.0 microseconds. The net result of using PAR5 instead of ATSBX on the BTO constant was a change of 0.4 microseconds, calculated before rounding. There was no appreciable change to the standard error.
6 Comparison of Estimates from Reduced and R-Channel Data Sets
When the optimum value for the T-channel offset is used it is expected that the resulting combined BTO constant would be equal to that obtained from restricting the estimate to the R-channel data alone, but that the standard deviations and standard errors would be different. As the reduced data set only retains eight T-channel data points, the impact of restricting estimation to the R-channel is expected to be modest.
| R-Channel | Reduced | |
| Offset δ | Not applicable | 4980.3 |
| K-bar | -495679.0 | -495679.0 |
| Standard deviation of K | 30.0 | 29.6 |
| Count | 54 | 62 |
| Standard error of K-bar | 4.09 | 3.75 |
Table 5: Comparison of R-Channel and time-interval Reduced estimates, based on PAR5 satellite vectors. Source: [5] (Statistics). All figures in microseconds.
Table 5 confirms that the same estimate for the mean BTO constant is obtained for the Reduced, and R-channel, data sets. The standard deviations are only slightly changed. The standard error of the R- channel data is larger, primarily due to the reduced sample size.
- A Second Look at the ATSB June Estimate
In section 2 it was concluded that the similarity between the ATSB’s estimated BTO constant given in [4] (Appendix G, Table 2) and our preliminary estimates was fortuitous. Similar values were obtained as our analysis was refined. The topic merits a second look and in this section we seek to quantify how likely the ATSB’s estimate may have been. We will employ risk analysis to assess the probability of obtaining differences of various magnitudes in the sample mean BTO constant.
The ATSB June estimate of the mean BTO constant was given as -495679(.3) microseconds and was based on only 17 out of 54 R- channel data points. The first decimal place has been calculated from the values in ATSB’s table. However as we have refined our modelling of the satellite location, in order to make a fair comparison we first need to recalculate ATSB’s mean BTO constant with our current set of satellite vectors.
Using the PAR5 satellite vectors, the mean BTO constant for ATSB’s selected 17 data points would be -495680.2 microseconds. This differs from the R-channel mean of -495679.0, reported in Section 6 above, by 1.2 microseconds. It is this 1.2 microsecond difference whose prior probability we seek to assess.
The question to be addressed by the risk analysis is how probable is it that 17 randomly-selected R-channel ground data points would lead to a mean BTO constant that is within 1.2 microseconds of the mean BTO obtained for a population of size 54? A simulation with one million iterations was conducted to obtain the distribution of sample means of BTO constants from random samples of size 17, chosen without replacement from the 54 available data points.
It transpired that a difference of 1.2 microseconds or less would occur for about 15% of the samples. So the odds are clearly against observing a value this close, confirming our initial conclusion that the similarity was fortuitous. On the other hand, 15% is still an appreciable probability, and so this is not an entirely surprising outcome.
Using other outputs from the risk analysis, Table 6 gives the probabilities of observing specific differences in the mean BTO constant, for a range of alternative magnitudes.
| Difference in the sample mean K, microseconds | 0.5 | 1 | 1.5 | 2 | 3 | 4 |
| Probability in a sample of size 17 | 6.5% | 12.9% | 19.4% | 25.6% | 37.6% | 48.7% |
Table 6: Probabilities of obtaining close mean BTO constant values from random samples of size 17.
Table 6 tells us, for example, that a difference within 0.5 microseconds would occur with a probability of only 6.5%, while a difference that is within 2 microseconds would be expected in about one quarter of the random samples. Reference [7a] contains the original model that was used and requires the Palisade @RISK package. Reference [7b] contains the results of the risk analysis.
Conclusions
In this report we have demonstrated the sensitivity of the magnitude of the T-channel offset to the data set being adopted for calibration, but also that similar values for the BTO constant can be obtained provided T-channel offsets are re-estimated for the dataset being adopted. We have compared our preliminary estimates for the mean BTO constant with those published by the ATSB and obtained a close match with its published findings. However, the smallness of the ATSB’s sample suggests that a wide confidence band should have been placed on its estimate, and the similarity in our estimates of the mean is fortuitous. On the basis on the current analysis, a consistent estimate, with narrower confidence band, would be justified.
We then conducted a review of data from the T-channel, leading to the identification of a reduced data set for subsequent estimation. More robust estimates for the BTO constant were obtained from the reduced data set. We also studied the impact of using a new set of satellite vectors and made a comparison between estimates from the reduced data set and estimates based entirely on BTO data for the R-channel. Using a more extended data set that included the climb and early cruise phase, we also examined how the data reduction process could be refined.
Based on the reduced dataset, using the PAR5 satellite vectors, the mean value for the BTO constant was -495679 microseconds, with a standard error of the order of 4 microseconds. The 95% normal confidence limits for this estimate are from -495671 to -495687 microseconds. Using the improved PAR5 satellite vectors provided an opportunity to revisit the ATSB’s June estimate for the BTO constant. It was concluded that the odds were against ATSB obtaining a value that was within 1.2 microseconds of our current estimate. However the probability is not sufficiently small for this to be a particularly surprising result.
A possible topic for further investigation would be a validation of the mean BTO constant using the aerial data (i.e. data obtained whilst the aircraft was airborne, in the early part of the flight).
Acknowledgement: The authors wish to thank Michael Exner for many detailed comments on previous drafts of this report. Any errors or omissions remain the responsibility of the authors.
References
[1] Exner, M. L. (2014). Derivation of Net L band Propagation Delay and Range from MH370 BTO Values. MH370 Independent Group. Available online at: http://www.aqqa.org/MH370/models/exner/RT_VS_VT_Delay_2014-06-25.pdf
[2] Inmarsat plc UK (2014). MH370 Data Communication Logs. Available online at: http://www.dca.gov.my/mainpage/MH370%20Data%20Communication%20Logs.pdf
[3] Sladen, P. (2014). Consolidated ADS-B logs for MH370.
Available online at: https://github.com/sladen/inmarsat-9m-mro/tree/master/ads-b/
[4] MH370 – Definition of Underwater Search Areas. 26 June 2014. Australian Transport Safety Bureau. Available online at: http://www.atsb.gov.au/mh370/mh370-definition-of-underwater-search-areas.aspx
[5] Hyman, G., and Martin, B. (2014). Microsoft Excel model for BTO constant. MH370 Independent Group. Available online at: http://www.aqqa.org/MH370/models/BTO_constant_GHBSM06.xlsx
[6] Rydberg, H. (2014). PAR5 Vector Set for IOR 3F1, based on vectors in [4]. MH370 Independent Group. Available online at: http://bitmath.org/mh370/satellite-par5-ecef.txt.gz
[7a] Hyman, G., and Martin, B. (2014). Microsoft Excel model with a Palisade @RISK simulation for the mean BTO constant for 17 randomly sampled R-channel BTO constant point-estimates. MH370 Independent Group. Available online at: http://www.aqqa.org/MH370/models/BTO_resample17_ATSB-sim.xlsx
[7b] Hyman, G., and Martin, B. (2014). Microsoft Excel model with a Palisade @RISK simulation for the mean BTO constant for 17 randomly sampled R-channel BTO constant point-estimates: simulation outcomes. MH370 Independent Group. Available online at [41 MB]: http://www.aqqa.org/MH370/models/BTO_resample17_ATSB-simResults.xlsx